حل چند چالش جاوا اسکریپتی از LeetCode

اگر در فضای حل چالش های برنامه نویسی، سوالات استخدامی و سوالات الگوریتمی باشید به احتمال زیاد می دانید که حل آن ها برای بسیاری از افراد مشکل است اما اگر بتوانید با تمرین ذهن خود را به این دسته از سوالات عادت بدهید قطعا سطح شما به عنوان یک برنامه نویس ارتقاء پیدا می کند. در ایران نیز بسیاری از شرکت ها مانند دیجی کالا برای استخدام برنامه نویسان خود از این دسته از سوالات استفاده می کنند بنابراین یادگیری روش حل آن ها برای شغل شما نیز مفید خواهد بود.

هشدار: سوالات مطرح شده در این مقاله از متوسط شروع شده و به پیچیده می رسند بنابراین فقط برای افرادی طراحی شده اند که به طور کامل با زبان جاوا اسکریپت آشنایی دارند.

بهتر است بدون مقدمه به سراغ حل این سوالات برویم.

۱. تبدیل عددنویسی رومی به عددنویسی امروزی

در روم باستان برای نوشتن اعداد از سیستم خاصی استفاده می کردند که امروزه به Roman Numerals یا عدد نویسی رومی شناخته می شود. این سیستم عدد نویسی ساده و قابل درک است:

مقدار       نماد

I             1

V             5

X             10

L             50

C             100

D             500

M             1000

همانطور که می بینید هر کدام از این نماد ها نماینده ی یک مقدار خاص است. مثلا برای نوشتن عدد یک از I (حرف i معادل یک) استفاده می کنیم، برای نوشتن عدد ۲ از II استفاده می کنیم، برای نوشتن ۳ از III استفاده می کنیم اما برای نوشتن عدد ۴ از IV استفاده می کنیم. چرا؟ در جدول بالا می بینید که هر نماد یک مقدار دارد و این مقدار ها در هر بازه ی خاص شکسته می شوند (بازه های ۱ تا ۵ تا ۱۰ تا ۵۰ تا ۱۰۰ تا ۵۰۰ تا ۱۰۰۰). از آنجایی I (یک) قبل از V (پنج) آمده است باید آن را از ۵ کم کنیم که مساوی با ۴ است. هر زمانی که نزدیک به بازه های بالا شویم این قانون صادق است:

• قرار دادن I (یک) قبل از V (پنج) معادل ۴ است.
• قرار دادن I (یک) قبل از X (۱۰) معادل ۹ است.
• قرار دادن X (ده) قبل از L (پنجاه) معادل ۴۰ است.
• قرار دادن X (ده) قبل از C (صد) معادل ۹۰ است.
• قرار دادن C (صد) قبل از D (پانصد) معادل ۴۰۰ است.
• قرار دادن C (صد) قبل از M (هزار) معادل ۹۰۰ است.

قوانین عددنویسی رومی بدین شکل است:

• هر نمادی که در سمت راست نماد دیگر قرار دارد، چنانچه مقدارش از آن نماد کمتر یا با آن مساوی باشد، ارزش آن نماد را زیاد می‌کند (مثال: XI = ۱۰+۱ = ۱۱).
• هر نمادی که در سمت چپ نماد دیگر قرار دارد، چنانچه مقدارش از آن کمتر باشد، ارزش آن نماد را کم می‌کند (مثال IX = ۱۰-۱ = ۹).
• هرگاه نمادی بین دو نماد بزرگ‌تر از خود قرار گرفته باشد، ابتدا با نماد سمت راستش ترکیب می‌شود، یعنی از ارزش آن می‌کاهد و بعد، طبق قانون اوّل، تفاضل بر ارزش نماد دیگر اضافه می‌شود (مثال XIV = (۵-۱)+۱۰ = ۱۴).

با این حساب از شما خواسته می شود کدی بنویسید که بتواند اعداد رومی را به اعداد امروزی تبدیل کند. به طور مثال III را گرفته و ۳ را برگرداند یا MCMXCIV را گرفته و 1994 را برگرداند. فرض سوال این است که رشته ی پاس داده شده به شما همیشه بین ۱ و ۱۵ کاراکتر خواهد بود و در بازه ی عددی ۱ تا ۳۹۹۹ هستند.

پاسخ به این سوال راحت است:

const symbols = {

  I: 1,

  V: 5,

  X: 10,

  L: 50,

  C: 100,

  D: 500,

  M: 1000,

};




const romanToInt = romanString => {

  let value = 0;

  for (let i = 0; i < romanString.length; i += 1) {

    symbols[romanString[i]] < symbols[romanString[i + 1]]

      ? (value -= symbols[romanString[i]])

      : (value += symbols[romanString[i]]);

  }

  return value;

};

بر اساس سه قانونی که برایتان توضیح دادم می توان گفت که باید بزرگی یا کوچکی حروف رومی را با یکدیگر مقایسه کنیم. برای این کار کافی است یک حلقه ی for را داشته باشیم و شروع به چرخش روی تک تک کاراکتر های رشته ی romanString کنیم. در صورتی که یک حرف کوچکتر از حرف بعدی (ایندکس بعدی) خود بود باید value را از آن کم کنیم اما اگر کمتر بود باید آن را با مقدار عددی اش جمع ببندیم. شما می توانید به همین راحتی به این سوال جواب بدهید.

نکته: برای حل این سوالات ده ها روش مختلف وجود دارد. تا زمانی که به پاسخ صحیح برسید، جواب شما هم مقبول است و لزومی ندارد که با پاسخ من یکی باشد.

۲. طولانی ترین پیشوند مشترک

این سوال بسیار ساده است: تابعی بنویسید که طولانی ترین پیشوند مشترک را از آرایه ای از رشته ها پیدا کند. در صورتی که پیشوند مشترکی بین اعضای آرایه نبود، تابع باید یک رشته ی خالی را برگرداند. به مثال زیر توجه کنید:

strs = ["flower","flow","flight"]

بین سه رشته ی موجود در این آرایه حروف ابتدایی fl مشترک هستند بنابراین تابع شما باید رشته ی fl را برگرداند. فرضیات سوال این است که طول رشته همیشه بین ۱ تا ۲۰۰ کاراکتر بوده و تمام کاراکتر ها همیشه با حروف کوچک انگلیسی نوشته می شوند.

من پاسخ این سوال را ابتدا به صورت ابتدایی به شما نشان می دهم و سپس از یکی از قابلیت های عالی جاوا اسکریپت استفاده خواهیم کرد:

const wordList = ["flower", "flow", "flight"];




const longestCommonPrefix = strings => {

  if (!strings.length) return "";




  for (let i = 0; i < strings[0].length; i++) {

    for (let str of strings) {

      if (str[i] !== strings[0][i]) {

        return str.slice(0, i);

      }

    }

  }




  return "";

};

ما در این مثال دو حلقه را داریم که به صورت تو در تو قرار گرفته اند. در حلقه ی اول فقط روی کاراکتر های اولین کلمه از آرایه ی پاس داده شده گردش کرده ایم. چرا؟ به دلیل اینکه طولانی ترین پیشوند مشترک به اندازه ی کوتاه ترین کلمه ی درون آرایه است بنابراین تفاوت ندارد روی کدام کلمه گردش کنیم. مثلا می توانستیم از دومین کلمه شروع کنیم اما همیشه مطمئن هستیم که اولین کلمه وجود خواهد داشت بنابراین خیالمان از این جهت راحت است. در حلقه ی دوم بین اعضای آرایه ی پاس داده شده گردش کرده ایم و گفته ایم اگر اولین کاراکتر از کلمه ی اول با کاراکتر i اُم از کلمات بعدی یکسان نبود یعنی دیگر پیشوند مشترکی وجود ندارد بنابراین از ابتدای کلمه تا ایندکس i اُم را برش زده و برمی گردانیم.

روش بالا برای افراد مبتدی قابل درک تر است اما ما می توانیم از روش پیشرفته تری نیز استفاده کنیم. همانطور که می دانید در جاوا اسکریپت متدی به نام reducer وجود دارد که روی آرایه ها اجرا شده و اعضای آن ها را به یک مقدار تقلیل می دهد. ما می توانیم از این متد برای حل این مسئله استفاده کنیم:

const wordList = ["flower", "flow", "flight"];




const longestCommonPrefix = strings => {

  if (strings === undefined || strings.length === 0) {

    return "";

  }




  return strings.reduce((acc, curr) => {

    let i = 0;

    while (acc[i] && curr[i] && acc[i] === curr[i]) i++;

    return acc.slice(0, i);

  });

};

تابعی که به reduce پاس داده می شود روی تک تک اعضای آرایه ی ما اجرا می شود. این تابع خودش دو آرگومان دارد:

• accumulator: مقداری است که در گردش قبلی (روی عضو قبلی آرایه) برگردانده می شود. در گردش اول به صورت پیش فرض صفر یا یک رشته ی خالی است.
• current: برابر با عضو آرایه در گردش فعلی است.

من گفته ام تا زمانی که کاراکتر i اُم از acc (رشته ی قبلی) و کاراکتر i اُم از رشته ی فعلی خالی نباشند و همچنین با هم برابر باشند یک واحد به متغیر i اضافه شود. در نهایت رشته ی نهایی (acc) را تا همان قسمت خاص برش می زنیم و برمی گردانیم. این مقدار برگردانده شده برابر با accumulator در گردش بعدی است. همانطور که گفتم accumulator در گردش اول برابر با صفر یا یک رشته ی خالی است.

۳. پرانتزهای معتبر

با فرض اینکه رشته ای از پرانتزها و براکت ها (علامت های () و [] و {}) داشته باشیم، کدی بنویسید که معتبر بودن ترتیب آن ها را مشخص کند. یک رشته زمانی معتبر است که:

• پرانتزها یا براکت های باز شده باید با همان نوع پرانتز یا براکت بسته شوند.
• پرانتزها یا براکت های باز شده باید با همان ترتیب پرانتز یا براکت بسته شوند.

به طور مثال رشته ی "()" معتبر و رشته ی "[)" نامعتبر است چرا که در دومی پرانتز با یک براکت بسته شده بنابراین «نوع» صحیح نیست. همچنین رشته ی "()[]{}" معتبر و رشته ی "([)]" نامعتبر است چرا که ترتیب بسته شدن براکت و پرانتز در آن صحیح نیست.

این تمرین در ظاهر ساده است اما ریزه کاری هایی دارد که شاید به چشمتان نیاید. سعی کنید خودتان به آن جواب داده و سپس به پاسخ من توجه کنید:

const isValid = string => {

  const stack = [];




  for (let i = 0; i < string.length; i++) {

    let character = string.charAt(i);

    switch (character) {

      case "(":

        stack.push(")");

        break;

      case "[":

        stack.push("]");

        break;

      case "{":

        stack.push("}");

        break;

      default:

        if (character !== stack.pop()) {

          return false;

        }

    }

  }




  return stack.length === 0;

};

ما یک آرایه ی ساده را در همان ابتدا تعریف کرده ایم و سپس روی کاراکتر های مختلف رشته ی پاس داده شده گردش خواهیم کرد. همانطور که در کد های بالا مشخص است من با استفاده از متد جاوا اسکریپتی charAt کاراکتر مورد نظر در گردش فعلی را گرفته و در متغیری به نام character ذخیره می کنم و سپس دستور switch خود را داریم.

در دستور switch فقط حالت های باز کردن پرانتز و براکت را داریم که سه عدد هستند. چرا؟ به دلیل اینکه پیش فرض سوال همین بود. هیچگاه نمی توانیم با پرانتز یا براکت بسته شروع کنیم. اگر چنین کاری را انجام بدهیم چطور می توانیم آن را ببندیم؟ پرانتز بسته شده که دوباره بسته نمی شود. در حالت های عادی (سه case اول) پرانتز یا براکت معادل و بسته ی آن را به آرایه اضافه می کنیم. اگر رشته با پرانتز و براکت بسته شروع شده باشد نیز وارد حالت default می شویم. این حالت متد pop را صدا می زند که آخرین عضو آرایه را حذف کرده و به ما برمی گرداند. من گفته ام اگر آخرین عضو آرایه برابر با کاراکتر فعلی نبود باید سریعا false برگردانده شود. چرا؟ برای درک این موضوع ابتدا باید حالت سالم را بررسی کنیم.

اگر رشته ای مانند "()" به ما پاس داده شود ابتدا ")" را داریم بنابراین "(" درون آرایه ی tack ثبت می شود. حالا وارد گردش دوم حلقه می شویم و به "(" می رسیم بنابراین وارد بخش default می شویم چرا که هیچ کدام از سه case اول مطابق با آن نیستند. در بخش default متد pop صدا زده می شود و آخرین عضو آرایه که همان "(" می باشد حذف شده و به ما برگردانده می شود. حالا ما در شرطمان گفته ایم اگر "(" برابر با کاراکتر فعلی ("(") نباشد باید false برگردانده شود. از آنجایی که "(" برابر با "(" است چنین شرطی صحیح نبوده و false برگردانده نمی شود. در حال حاضر متد pop آخرین عضو آرایه را حذف کرده است که تنها عضو نیز بوده است بنابراین حالا آرایه خالی است. اگر stack.length برابر صفر باشد true برگردانده می شود که یعنی رشته صحیح بوده است.

حالا فرض کنید رشته ی "())" به ما داده شود. ابتدا ")" را داریم که با case اول منطبق است بنابراین به آرایه اضافه می شود. سپس در گردش بعدی دوباره ")" را داریم (کاراکتر دوم رشته در گردش دوم) بنابراین باز هم به آرایه اضافه می شود. در حال حاضر آرایه به شکل زیر است:

[ ')', ')' ]

سپس به کاراکتر "(" می رسیم که به هیچ case ای منطبق نیست بنابراین وارد default می شود. در این بخش عضو آخر pop می شود و یک عضو در آرایه باقی می ماند. با این حساب دیگر stack.length برابر صفر نبوده و نتیجه false خواهد بود.

امیدوارم متوجه این پاسخ شده باشید. در ضمن یادتان باشد که روش های مختلفی برای حل این مسئله وجود دارد. به طور مثال کد زیر یک پاسخ دیگر به این سوال است:

const isValid = string => {

  const stack = [];

  const complement = {

    "(": ")",

    "{": "}",

    "[": "]",

  };




  for (let char of string) {

    if (complement[char]) stack.push(char);

    else if (stack.pop() === complement[char]) return false;

  }

  return stack.length === 0;

};

منطق این بخش نیز دقیقا مانند منطق سوال قبل اما بدون switch است. همچنین یک پاسخ دیگر برای این سوال:

if (s.length === 0) return true

if (s.length === 1) return false

if (s.length % 2 !== 0) return false




const dictionary = {

                '}': '{',

                ')': '(',

                ']': '['

}

const stack = []




for (let i = 0; i < s.length; i++) {

                const currChar = s[i]

                const lastChar = stack[stack.length - 1]

                const delChar = dictionary[currChar]




                if (delChar) {

                                if (delChar === lastChar) {

                                                stack.pop()

                                } else {

                                                return false

                                }

                } else {

                                stack.push(currChar)

                }

}




return !stack.length

این روش کمی طولانی تر است اما شاید درک آن برایتان راحت تر باشد.

۴. ادغام دو لیست پیوندی مرتب

با فرض اینکه دو لیست پیوندی مرتب شده را داریم کدی بنویسید که این دو لیست را به صورت مرتب شده با هم ادغام کند. در واقع می خواهیم اعضای اول از هر لیست با هم ادغام شوند، سپس اعضای دوم با هم ادغام شوند و سپس اعضای سوم و الی آخر. تصویر زیر به درک این موضوع کمک می کند:

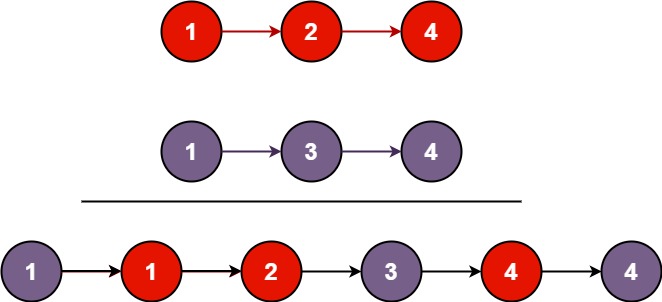
این سوال فرض می کند که اعضای لیست اول و دوم هیچ گاه نزولی نخواهند بود و همیشه اضافه می شوند. طبیعتا ما در جاوا اسکریپت داده ساختاری به نام لیست پیوندی نداریم بنابراین می توانیم برای حل این سوال از یک شیء ساده استفاده کنیم که دو خصوصیت val و next را داشته باشد. لیست های پیوندی یک مقدار val (مقدار یک node) و یک خصوصیت next را دارند که به node بعدی اشاره می کند.

نکته: برای حل این سوال باید با داده ساختار لیست های پیوندی آشنا باشید.

برای حل این سوال ابتدا فرض کنید دو لیست پیوندی به شکل زیر داریم:

1 -> 2 -> 4

1 -> 3 -> 4

هر دو لیست مرتب شده هستند. برای حل این سوال ابتدا یک لیست پیوندی را می سازیم که یک مقدار اولیه داشته باشد. چرا؟ به دلیل اینکه باید یک لیست پیوندی اولیه داشته باشیم که مقادیر را به صورت مرتب شده در آن قرار بدهیم. همانطور که گفتم من از یک شیء برای این کار استفاده می کنم:

const mergeTwoLists = (l1, l2) => {

  let dummyNode = { val: -1, next: null };

  let head = dummyNode;




  while (l1 !== null && l2 !== null) {

    if (l1.val <= l2.val) {

      dummyNode.next = l1;

      l1 = l1.next;

    } else {

      dummyNode.next = l2;

      l2 = l2.next;

    }




    dummyNode = dummyNode.next;

  }




  if (l1 !== null) {

    dummyNode.next = l1;

  } else {

    dummyNode.next = l2;

  }




  return head.next;

};

مقدار اولیه ی لیست پیوندی من (val) روی ۱- تنظیم شده است اما شما می توانید هر مقداری را برایش بگذارید. مقدار اولیه فقط برای شروع کار است و معمولا برنامه نویسان از عدد ۱- استفاده می کنند بنابراین من هم همین کار را کرده ام. در ضمن از یک متغیر به نام head استفاده کرده ایم تا به dummyNode (لیست پیوندی اولیه) اشاره کند. چرا؟ در ادامه خواهید دید که dummyNode دائما روی node های مختلف جا به جا می شود اما ما نهایتا می خواهیم کل dummyNode را از ابتدای آن به عنوان نتیجه برگردانیم بنابراین نیاز است که به ابتدایش دسترسی داشته باشیم.

در مرحله ی بعدی یک حلقه ی while را داریم که می گوید تا زمانی که l1 (لیست اول) و l2 (لیست دوم) وجود داشته باشند باید گردش کنیم. در هر گردش دو شرط if را داریم: اگر مقدار عضو اول از لیست اول (l1.val) کمتر یا مساوی با مقدار عضو اول از لیست دوم (l2.val) باشد باید node بعدی (همان خصوصیت next) در dummyNode خود را روی l1 تنظیم کنیم و سپس l1 را یک node به جلو ببریم (با صدا زدن l1.next). چرا؟ به دلیل اینکه باید عضو کوچکتر اول باشد (قرار بر ایجاد یک لیست پیوندی مرتب بود). برعکس این کار را نیز برای l2 انجام می دهیم. پس از شرط if به انتهای حلقه می رسیم بنابراین باید dummyNode را یک عضو (یک node) به جلو ببریم تا در گردش بعدی دوباره روی همان عضو قبلی باقی نمانیم.

پس از آنکه از حلقه ی while خارج شدیم یعنی یکی از دو لیست به انتهای خود رسیده است. با این حساب باید لیست باقی مانده را به dummyNode اضافه کنیم. اگر l1 باقی مانده بود (null نبود) آن را به عنوان next به dummyNode می دهیم. برعکس این کار را برای l2 نیز انجام می دهیم. در نهایت head.next را برمی گردانیم. چرا؟ head در ابتدا به dummyNode اشاره می کرد. اولین node یا همان اولین عضو head، عدد ۱- است که جزئی از دو لیست نیست و فقط به عنوان مقدار اولیه از آن استفاده کرده ایم بنابراین نباید آن را برگردانیم بلکه تمام اعضای بعد از آن باید برگردانده شوند. به همین دلیل است که head.next (عضو بعد از ۱-) را برگردانده ایم.

۵. حذف عناصر تکراری از آرایه ی مرتب شده

با فرض اینکه آرایه ای به نام nums وجود دارد که اعضایش به صورت صعودی مرتب شده اند، کدی بنویسید که اعضای تکراری را با حفظ ترتیب حذف کند. در نظر داشته باشید که اجازه ی استفاده از مموری برای ساخت یک آرایه ی جدید را ندارید بلکه باید همان آرایه ی پاس داده شده را مستقیما ویرایش کنید.

همچنین اگر تعداد k عضو یکتا پس از ویرایش آرایه باقی مانده باشند، تابع شما باید k را برگرداند. بگذارید برایتان یک مثال بزنم. فرض کنید ورودی به تابع شما (آرایه ی پاس داده شده) بدین شکل باشدک

nums = [1,1,2]

در این آرایه دو عدد یکتا (غیرتکراری) داریم (۱ و ۲) بنابراین k برابر با ۲ است. تابع ما باید آرایه ی پاس داده شده را بدین شکل ویرایش کند:

[1,2,_]

عضو آخر (علامت _) به معنی این است که اهمیتی ندارد پس از پاسخ چه مقادیری قرار بگیرد. پس از این کار نیز تابع باید عدد k را برگرداند که همان ۲ می باشد.

برای حل این سوال ابتدا باید به نکته ی بسیار مهمی توجه کنیم: آرایه ی پاس داده شده به ما به صورت صعودی مرتب شده است بنابراین مقادیر تکراری باید حتما پشت سر هم آمده باشند. نکته ی بعدی اینجاست که عدد اول همیشه یکتا است. مثلا اگر آرایه ی [1,1,2] را داشته باشیم می دانیم که عدد اول (۱) همیشه یکتا است بنابراین عملیات را باید از ایندکس ۱ شروع کنیم و با ایندکس صفر کاری نداریم.

با این حساب پاسخ به این سوال بسیار ساده می شود:

const removeDuplicates = nums => {

  let index = 1;




  for (let i = 0; i < nums.length - 1; i++) {

    if (nums[i] !== nums[i + 1]) {

      nums[index++] = nums[i + 1];

    }

  }




  return index;

};

من در ابتدا متغیری به نام index را دارم که مقدارش برابر با ۱ است. همانطور که گفتم عدد اول همیشه یکتاست بنابراین وارد کردن اعداد را از عدد دوم (ایندکس اول) شروع می کنیم. ما در اینجا یک حلقه داریم که می خواهیم در آن هر عدد را با عدد بعدی خودش مقایسه کنیم. هر گاه یک عدد با عدد بعدی خودش تفاوت داشت یعنی آن عدد یکتاست بنابراین آن را وارد آرایه می کنیم. اگر دقت کنید من در شرط ادامه ی حلقه گفته ام تا زمانی که i کوچکتر از طول آرایه ی nums منهای یک باشد. چرا؟ به دلیل اینکه ما همیشه یک عدد را با عدد بعدی اش مقایسه می کنیم بنابراین اگر تا آخرین عضو آرایه برویم دیگر عدد بعد از آن وجود نخواهد داشت (عدد بعد از عدد آخر یک خطای منطقی است!). از طرفی من اعداد یکتا را در ایندکس index ذخیره می کنم اما یک واحد آن را افزایش داده ام تا همان ایندکس تکراری را در هر گردش ویرایش نکنیم.

بیایید همان مثال آرایه ی [1,1,2] را در نظر بگیریم. در گردش اول می گوییم آیا عدد اول (۱) با عدد دوم (۱) تفاوت دارد؟ خیر! بنابراین رد می شویم و کاری انجام نمی دهیم. در گردش دوم می گوییم آیا عدد دوم (۱) با عدد سوم (۲) تفاوت دارد؟ بله! بنابراین عدد سوم (۲) را وارد ایندکس ۱ (عدد دوم) می کنیم. با این حساب عدد ۱ که قبلا عضو دوم آرایه بود با عدد ۲ جایگزین می شود. در این حالت آرایه برابر با [1,2,2] خواهد بود و حلقه تمام می شود. همانطور که گفتم هیچ اهمیتی ندارد که بعد از پاسخ (اعداد ۱ و ۲ - تا ایندکس k) چه اعداد و مقادیری بیایند.

۶. حذف تمام اعضای تکراری

با فرض اینکه آرایه ای به نام nums و عددی به نام val، باید کدی بنویسید که تمام اعضای برابر با val را از آرایه ی nums حذف کنند. این مسئله باید به روش in-place حل شود یعنی اجازه ی مصرف مموری اضافه برای ساخت یک آرایه ی جدید را نداشته و باید همان آرایه ی پاس داده شده را ویرایش کنید. در نهایت باید مانند مثال قبل k را برگردانید که تعداد اعضای باقی مانده در آرایه است. تفاوت این سوال با سوال قبل در اینجاست که اعضای آرایه مرتب نشده اند و نیازی هم به مرتب شدن ندارند.

پاسخ به این سوال بسیار ساده است:

const removeElement = (nums, val) => {

  for (let i = 0; i < nums.length; i++) {

    if (nums[i] === val) {

      nums.splice(i--, 1);

    }

  }

  return nums.length;

};

در این سوال من بین تک تک اعضای آرایه ی nums گردش کرده ام و هر کدام که برابر با آن بوده است را با متد splice حذف کرده ام. اما توجه داشته باشید که یک واحد از i کم کرده ام (--i). چرا؟ به دلیل اینکه با حذف شدن یک عنصر تمام عناصر آرایه یک واحد به سمت چپ منتقل می شوند بنابراین باید در گردش بعدی روی همین ایندکس بمانیم چرا که اگر به ایندکس بعدی برویم اعداد نیز به چپ منتقل می شوند و بنابراین یک عدد را به طور کامل جا می گذاریم.

۷. پیاده سازی تابع strStr از زبان ++C

اگر با زبان ++C کار کرده باشید می دانید که در آن تابعی به نام strStr وجود دارد. این تابع دو آرگومان می گیرد:

• needle(سوزن): رشته ای که باید درون پشته ی کاه پیدا شود.
• haystack (پشته ی کاه): یک رشته ی طولانی که باید در آن به دنبال سوزن باشیم.

ما از شما می خواهیم که این متد را در جاوا اسکریپت پیاده سازی کنید به طوری که اولین ایندکس از سوزن که درون پشته ی کاه پیدا شده را برگردانید. در صورتی که سوزن در پشته ی کاه وجود نداشت عدد ۱- و در صورتی که سوزن یک رشته ی خالی بود عدد صفر را برگردانید. مثال:

haystack = "hello"

needle = "ll"

Output: 2

چرا ۲؟ به دلیل اینکه حرف l (اولین حرف needle که در haystack پیدا شده است) ایندکس ۲ را دارد.

برای حل این سوال دو راه اصلی داریم: راه اول اینکه از متد های آماده مانند indexOf و search در جاوا اسکریپت استفاده کنیم و راه دوم اینکه از متد های آماده استفاده نکنیم. من هر دو حالت را به شما نشان می دهم.

راه ساده:

const strStr = (haystack, needle) => {

  if (needle === "") return 0;




  const result = haystack.indexOf(needle);




  return result;

};

این روش آنچنان ساده است که نیای به توضیح ندارد اما با این کار دیگر معمایی نداریم و سوال دیگر چالش نیست. برای اینکه واقعا آن را به چالش تبدیل کنیم باید از تمام متد های آماده دوری کرده و الگوریتم خودمان را بنویسیم:

const strStr = (haystack, needle) => {

  let needleLength = needle.length;

  let haystackLength = haystack.length;




  if (needle === "") return 0;

  if (haystackLength < needleLength) return -1;




  for (let i = 0; i <= haystackLength - needleLength; i++) {

    if (haystack[i] === needle[0]) {

      let j;

      for (j = 0; j < needleLength; j++) {

        if (needle[j] !== haystack[i + j]) {

          break;

        }

      }

      if (j === needleLength) return i;

    }

  }




  return -1;

};

ما ابتدا طول سوزن و پشته ی کاه را محاسبه کرده و درون متغیر هایی قرار داده ایم. در مرحله ی بعدی دو شرط if را داریمکه اگر needle خالی بود عدد صفر و اگر طول سوزن بیشتر از پشته ی کاه بود عدد ۱- را برگردانیم.

در بخش بعدی یک حلقه ی for را داریم که به اندازه ی تفاوت اندازه ی رشته ی سوزن و پشته ی کاه گردش می کند. چرا؟ به دلیل اینکه نیازی نیست به اندازه ی کل پشته ی کاه گردش کنیم. مثلا اگر سوزن ۴ کاراکتر باشد اما به ۳ کاراکتر انتهایی پشته ی کاه رسیده باشیم قطعا می دانیم که به هیچ عنوان ممکن نیست سوزن در پشته ی کاه باشد به دلیل اینکه اصلا جای کافی برای آن نیست (سوزن در این مثال ۴ کاراکتر دارد در حالی که فقط ۳ کاراکتر از پشته باقی مانده است و طبیعتا ۴ کاراکتر در ۳ کاراکتر جا نمی شود).

درون این حلقه یک شرط ساده دارم که اگر اولین کاراکتر از سوزن درون پشته ی کاه پیدا شد باید یک حلقه ی دیگر را شروع کنیم. این حلقه روی سوزن گردش می کند. توجه کنید که من متغیر j را خارج از این حلقه ی دوم تعریف کرده ام چرا که می خواهم بعدا به آن دسترسی داشته باشم (در ادامه خواهید دید). ما این حلقه را ادامه می دهیم و در هر گردش یک واحد به j اضافه می شود. در صورتی که ایندکس j سوزن با ایندکس i + J در پشته یکی باشد که مشکلی نیست اما اگر یکی نباشند یعنی کارمان تمام شده است بنابراین از حلقه break می کنیم (خارج می شویم). حالا اگر j با طول سوزن برابر باشد باید همان i را برگردانیم چرا که اولین ایندکس ما است. در غیر این صورت همان عدد ۱- برگردانده می شود.

بگذارید این کد را با مثال توضیح بدهم. فرض کنید پشته ی کاه roxo بوده و سوزن نیز xo است. در چنین حالتی ابتدا گردش روی پشته ی کاه را شروع می کنیم. ایندکس صفر از roxo (حرف r) با ایندکس صفر از سوزن (حرف x) برابر نیست بنابراین یک واحد به i اضافه شده و به گردش بعدی می رویم. ایندکس یک پشته (حرف o) با ایندکس صفر سوزن (حرف x) یکی نیست بنابراین به گردش بعدی می رویم. ایندکس دو پشته (حرف x) با ایندکس صفر سوزن (حرف x) یکی است بنابراین وارد حلقه ی دوم می شویم. در این حلقه می گوییم ایندکس j از سوزن (حرف x در گردشِ اول، چرا که j صفر است) آیا برابر ایندکس i + j در پشته است؟ i + j در گردش اول حلقه ی دوم برابر با 0 + 2 یا همان ۲ است. ایندکس ۲ از پشته x و ایندکس صفر از سوزن نیز x است بنابراین یک واحد به j اضافه شده و به گردش بعد در حلقه ی دوم منتقل می شویم. حالا j برابر ۱ است. ایندکس ۱ از سوزن (حرف o) برابر با ایندکس i + j (در این حلقه برابر با 1 + 2) از پشته (حرف o) است بنابراین یک واحد به j اضافه می کنیم اما وارد گردش بعدی نمی شویم چرا که j از طول سوزن بیشتر شده است. در این حالت i برابر ۲ و j برابر ۱ است. اگر j (عدد ۱) برابر طول سوزن باشد یعنی تمام کاراکتر های آن بخش را پیدا کرده ایم بنابراین ایندکس ما همان i (عدد ۲) است که باید برگردانده شود.

۸. ایندکس ثبت

با فرض اینکه آرایه ای مرتب شده از اعداد صحیح داشته باشیم و یک عدد را به شما بدهیم، کدی بنویسید که ایندکس این عدد را برگرداند اما اگر عدد در آرایه وجود نداشت ایندکسی را برگرداند که آن عدد در هنگام اضافه شدن به آرایه باید دریافت کند. در نظر داشته باشید که الگوریتم نوشته شده توسط ما باید از نظر زمان (O(log n باشد.

در حالت عادی ممکن است بخواهید با یک حلقه از ابتدای آرایه شروع کرده و تک تک اعداد را چک کنید اما انجام چنین کاری قبول نمی شود. چرا؟ به دلیل اینکه گفته ایم الگوریتم ما از نظر زمان باید در دسته ی (O(log n قرار بگیرد در حالی که نوشتن یک حلقه و گردش روی تک تک اعداد آرایه از نوع (n)O است. من برای حل این سوال یک راهنمایی می کنم: باید از الگوریتم Binary Search استفاده کنید. من پیشنهاد می کنم خودتان سعی کنید این سوال را حل کنید و سپس به پاسخ من نگاه کنید.

همانطور که گفتم برای حل این سوال از الگوریتم Binary Search استفاده می کنیم. در این الگوریتم به جای آنکه از سمت راست یا چپ آرایه شروع کرده و تک تک اعضای آرایه را بررسی کنیم، باید از وسط آرایه شروع کنیم! برای به دست آوردن وسط آرایه نیز باید ایندکس اول (صفر) را با ایندکس آخر جمع کرده و نتیجه را تقسیم بر ۲ کنید. به مثال زیر توجه کنید:

const nums = [1, 3, 5, 6];

برای حل سوال یک نشانگر برای مشخص کردن ابتدای آرایه و یک نشانگر برای مشخص کردن انتهای آرایه می خواهیم. نام نشانگر ابتدا را L  (مخفف Left) و نام نشانگر انتها را R (مخفف Right) می گذاریم:

[1, 3, 5, 6];

L             R

در حال حاضر L روی ۱ و R روی ۶ است. در این آرایه ایندکس اول صفر و ایندکس آخر ۳ است. برای به دست آوردن وسط آرایه L + R را بر ۲ تقسیم می کنیم: صفر + ۳ برابر با ۳ است که اگر آن را تقسیم بر ۲ کنیم عدد ۱.۵ به دست می آید. طبیعتا ایندکس اعشاری وجود ندارد بنابراین آن را به پایین گرد می کنیم. من وسط را ایندکس ۱ در نظر می گیرم که عضو دوم (عدد ۳) است. این نشانگر سوم ما است که نامش را M (مخفف Middle به معنی «وسط») می گذاریم:

[1, 3, 5, 6];

L  M     R

با این حساب از عدد ۳ شروع می کنیم. فرض کنید عدد پاس داده شده به ما ۵ باشد. آیا ۳ با ۵ یکی است؟ خیر. از طرفی می دانیم که آرایه مرتب شده است و ۳ کمتر از ۵ است بنابراین باید به سمت راست برویم (به دنبال مقدار بزرگتری از ۳ هستیم). برای انجام این کار نشانگر L را به سمت راست و بعد از M می آوریم:

[1, 3, 5, 6];

    M  L  R

حالا L روی ایندکس ۲ (عدد ۵) قرار دارد بنابراین باید M را دوباره محاسبه کنیم: ۲ + ۳ تقسیم بر ۲ برابر با ۲.۵ است که آن را به پایین گرد می کنیم و عدد ۲ را می گیریم. حالا آیا ۵ برابر با M (مقدار ۵) است؟ بله! بنابراین به جواب رسیده ایم و ایندکس ۲ را برمی گردانیم.

این پاسخ برای مواقعی است که عدد مورد نظر در آرایه وجود داشته باشد. اگر عدد وجود نداشت چطور؟ مثلا فرض کنید عدد مورد نظر ۲ است:

[1, 3, 5, 6];

L   M      R

مثل دفعه ی قبل L و R و M را مشخص می کنیم. حالا می گوییم آیا ۲ (عدد مورد نظر) برابر با M (مقدار ۳) است؟ خیر، از آن کوچکتر است بنابراین باید به سمت چپ حرکت کنیم. با این حساب باید R را به قبل از M حرکت بدهیم:

[1, 3, 5, 6];

L   M     

R

حالا L و R هر دو روی یک ایندکس قرار گرفته اند بنابراین متوجه می شویم که وسطی وجود ندارد و عدد مورد نظر در آرایه ی ما وجود ندارد. با این حساب ایندکس برگردانده شده باید 1 + L باشد (بعد از ۱ و قبل از ۳).

حالا که توضیحات کلی از جست و جوی باینری را به شما دادم بهتر است شروع به کدنویسی کنیم:

const searchInsert = (nums, target) => {

  let L = 0;

  let R = nums.length - 1;

  let M;




  while (L <= R) {

    M = Math.floor((L + R) / 2);




    if (nums[M] === target) return M;




    if (target > nums[M]) L = M + 1;

    if (target < nums[M]) R = M - 1;

  }

  return L;

};

همانطور که می بینید در ابتدای این تابع متغیر های L و R و M را تعریف کرده ایم. در بخش بعدی یک حلقه ی while را داریم که تا زمانی که L از R کوچک تر یا مساوی باشد اجرا می شود. چرا باید کوچک تر باشد؟ به دلیل اینکه آرایه ی ما مرتب شده است بنابراین ممکن نیست اعداد سمت چپ از راست بزرگتر باشند. اگر target (عدد مورد نظر) برابر با عددی است که ایندکس M را دارد در همان ابتدا ایندکس M را برمی گردانیم. در صورتی که اینطور نباشد باید به دو شرط بعدی برویم:

• هدف کوچکتر از عضوی با ایندکس M است. در این صورت طبق توضیحاتی که دادم باید L را به بعد از M منتقل کنیم.
• هدف بزرگ تر از عضوی با ایندکس M است. در این صورت طبق توضیحاتی که دادم باید R را به قبل از M منتقل کنیم.

در نهایت به جایی می رسیم که L بزرگ تر از R می شود بنابراین دیگر نمی توانیم در حلقه گردش کنیم و L را برمی گردانیم. چرا L؟ این مسئله را در قالب یک مثال برایتان توضیح می دهم. فرض کنید آرایه ی شما فقط یک عضو داشته باشد و عدد هدف نیز ۱ باشد:

const nums = [2]

حالا L و R و M همگی روی ۲ هستند اما عدد هدف ۱ است بنابراین باید R را به قبل از M ببریم. با این کار R قبل از L خواهد بود و همانطور که گفتم این مسئله در آرایه ی مرتب شده غیر ممکن است. در این حالت L را برمی گردانیم که ایندکس صفر است و عدد هدف (۱) نیز باید روی ایندکس صفر اضافه شود.

در حالت دیگر اگر همین آرایه را با عدد هدف ۳ داشته باشیم چطور؟ در این حالت L را بعد از R قرار می دهیم که باز هم غیر ممکن است بنابراین حلقه ی while متوقف می شود. چرا باید L را برگردانیم؟ به دلیل اینکه در این حالت L برابر ۱ است (عضو دوم) و عدد هدف (۳) نیز باید بعد از تنها عضو آرایه (عدد ۲) قرار بگیرد که ایندکس ۱ است.

۹. بزرگترین زیرآرایه

با فرض اینکه یک آرایه به نام nums داشته باشیم، بدون تغییر ترتیب اعضای آرایه یا شکستن آن ها، زیرآرایه ای را از nums استخراج کنید که جمع اعضای آن بزرگترین مقدار ممکن را داشته باشد و در نهایت این مجموع نهایی را برگردانید. به طور مثال آرایه ی زیر را در نظر داشته باشید:

nums = [-2,1,-3,4,-1,2,1,-5,4]

بزرگترین زیرآرایه ی آن آرایه ی [4,-1,2,1] است و مجموع اعضایش ۶ می باشد بنابراین تابع شما باید ۶ را برگرداند. زیرآرایه ی پیدا شده توسط شما باید حداقل یک عضو داشته باشد. توجه داشته باشید که زیرآرایه ی شما باید یک توالی بدون تقطیع از آرایه ی اصلی باشد.

من برای حل این سوال سه راه حل را به شما نشان می دهم. ساده ترین حالت حل این سوال که از نظر سرعت و بهینه بودن بدترین حالت حل این سوال است شامل امتحان کردن تمام حالت های ممکن خواهد بود. چطور؟ یعنی ابتدا از عضو اول شروع می کنیم (عدد ۲-) و از ۲- تا ۱ (عضو بعدی) می رویم. این یک زیر‌ آرایه است. در مرحله ی بعدی از ۲- تا ۳- می رویم که یک زیر آرایه ی دیگر است و الی آخر.  این کار را آنقدر انجام می دهیم تا تمام زیرآرایه های ممکن را حساب کنیم. در این حالت به سه حلقه ی for نیاز داریم: حلقه ی اول برای گردش در کل آرایه، حلقه ی دوم برای گردش در زیر آرایه (مشخص کردن آخرین مقدار زیر آرایه) و حلقه ی سوم برای گردش بین اعضای زیرآرایه و محاسبه ی مجموع اعضای آن! این روش از نظر Big O از نوع O(N³) است که یعنی به هیچ عنوان بهینه نیست.

روش دوم بدین شکل است که در هنگام محاسبه ی زیرآرایه، مقدار (مجموع اعضای) زیر آرایه ی قبلی را در یک متغیر ذخیره کنیم و آن را با حالت قبلی مقایسه کنیم. در این حالت به یک حلقه ی for برای گردش در آرایه ی اصلی و یک حلقه ی دیگر برای گردش در زیر آرایه نیاز داریم. یعنی آخرین حلقه را حذف کرده ایم چرا که مقدار زیر آرایه را در متغیری ذخیره کرده ایم. این روش از نظر Big O از نوع O(N²) است که تا حد مناسبی بهینه تر شده است اما هنوز هم بهینه نیست.

روش سوم که بهترین روش است با کنار زدن اعداد منفی کار می کند. دوباره به آرایه ی زیر توجه کنید:

nums = [-2,1,-3,4,-1,2,1,-5,4]

در این آرایه از عدد اول (۲-) شروع می کنیم و به عدد دوم (۱) می رسیم. این اولین زیرآرایه ی ما است و مجموع اعضای آن ۲- و ۱ برابر با ۱- است. هر زمان که مجموع دو مقدار قبلی منفی باشد آن مقادیر را حذف می کنیم. چرا؟ به دلیل اینکه یک عدد مثبت به تنهایی بیشتر از تمام این مقادیر است. طبیعتا زمانی که می خواهیم بزرگترین زیر آرایه را حساب کنیم اعداد منفی هیچ کمکی به ما نمی کنند بنابراین به جای آنکه زیر آرایه ی دوم را دوباره از عدد ۲- شروع کنیم به طور کل عدد ۲- را حذف می کنیم و زیر آرایه ی بعدی از ۱ (عدد دوم) شروع می شود. حالا اولین زیرآرایه ی ما ۱ و ۳- است و مجموع اعدادشان ۲- می باشد. عدد بعدی ما ۴ می باشد (عضو چهارم آرایه ی اصلی) که به تنهایی از مجموع زیرآرایه ی قبلی (۱ و ۳-) بیشتر می باشد بنابراین تمام اعداد قبل از آن را به طور کل نادیده می گیریم.

در مرحله ی بعدی زیرآرایه را دوباره از ابتدا و با عدد ۴ شروع می کنیم. عدد بعد از ۴، عدد ۱- است و آن را نگه می داریم چرا که عدد قبل از آن ۴ بود که یک عدد مثبت است و مشکلی نداریم. مجموع ۴ و ۱- برابر با ۳ است. حالا عدد بعدی ۲ است و آن را هم نگه می داریم. توجه کنید که اگر ۱- را حذف کنیم، ۴ را نیز از دست می دهیم. چرا؟ به دلیل اینکه زیرآرایه ی ما باید یک توالی بدون تقطیع از آرایه ی اصلی باشد. مجموع ۴ و ۱- و ۲ برابر با ۶ می شود. عدد بعدی ۵- است و بعد از آن نیز عدد ۴ را داریم که با جمع کل آن ها (۴ و ۱- و ۲ و ۵- و ۴) به عدد ۵ می رسیم. این عدد از ۶ کمتر است بنابراین بزرگترین زیرآرایه همان مقدار قبلی است. این روش حل از نظر Big O برابر با O(n) است، یعنی از تمام روش های قبلی با تفاوت بیشتری بهینه تر است.

حالا که فلسفه ی  چالش را با توضیحات بررسی کردیم، بهتر است شروع به کدنویسی کنیم:

const maxSubArray = nums => {

  maxSub = nums[0];

  curSum = 0;




  for (let i = 0; i < nums.length; i++) {

    if (curSum < 0) curSum = 0;




    curSum += nums[i];

    maxSub = Math.max(maxSub, curSum);

  }




  return maxSub;

};

در ابتدا maxSub یا مجموع اعضای بزرگترین زیرآرایه را روی اولین عدد زیرآرایه می گذارم و curSum یا مجموع اعضای فعلی را نیز روی صفر می گذارم. این فقط یک مقدار دهی اولیه است و بعدا آن ها را تغییر می دهیم. در حلقه ای که می بینید در ابتدا یک شرط داریم: اگر مجموع اعضای فعلی منفی شد، مقدار curSum را دوباره روی صفر می گذاریم. سپس در هر گردش curSum را با عدد بعدی جمع می زنیم. همچنین Math.max را صدا زده ایم تا بین maxSub و curSum بزرگترین را انتخاب کنیم و برابر با maxSub قرار بدهیم. چرا؟ به دلیل اینکه جمع اعداد فعلی یا بزرگتر از maxSub است یا کوچکتر از آن. اگر به جمع بزرگترین رسیده ایم طبیعتا maxSub باید به این مقدار تغییر کند. پس از اینکه تا انتهای این رشته حرکت کردیم maxSub را برمی گردانیم که همان مجموع اعضای بزرگترین زیرآرایه است.

۱۰. طول کلمه ی آخر

حالا که سوالات نسبتا سختی را با هم حل کرده ایم بهتر است یک سوال ساده را نیز در نظر بگیریم. با فرض اینکه رشته ای از کلمات به نام s به شما پاس داده شده باشد، طول آخرین کلمه ی آن را محاسبه کنید. اگر رشته ی آخری وجود ندارد، عدد صفر را برگردانید. به طور مثال اگر رشته ی زیر را داشته باشیم:

s = "Hello World"

تابع شما باید عدد ۵ را برگرداند چرا که کلمه ی آخر (World) پنج حرف دارد. از طرفی اگر رشته ای خالی نیز به ما پاس داده شد عدد صفر را برایش برمی گردانیم.

حل این سوال بسیار ساده است و نباید بیش از حد به آن فکر کنید. در واقع من این کار را در یک خط ساده انجام می دهم:

const lengthOfLastWord = s => s.trim().split(" ").pop().length;

ابتدا تابع trim را صدا زده ایم تا اسپیس های ابتدایی و انتهایی رشته حذف بشوند. مثلا رشته ی "   Hello" به رشته ی "Hello" تبدیل شود. در مرحله ی بعدی split را صدا زده ایم تا کلمات را از هم جدا کرده و درون یک آرایه قرار بدهیم. در نهایت pop را صدا زده ایم که آخرین عضو از یک آرایه ی جاوا اسکریپتی را حذف می کند و به ما می دهد. حالا length را روی آخرین عضو حذف شده صدا می زنیم تا طول آن را به دست بیاوریم. به همین سادگی توانستیم این سوال را نیز حل کنیم.

منبع: وب سایت leetcode