ساخت یک شبکه عصبی در پایتون (راهنمای تصویری+کدهای مورد نیاز)

این مقاله راهنمایی ابتدایی برای درک عملکرد درونی یادگیری عمیق است. این مقاله هم چنین نظر ویراستاران Packt Publishing را به خود جلب کرده است. آن ها کتابی برای ساخت پروژه های شبکه عصبی با پایتون منتشر کرده اند. این کتاب را می توانید از این نشانی تهیه کنید. این کتاب ادامه این مقاله است و اجرای پروژه های شبکه عصبی را در زمینه هایی مانند تشخیص چهره، تحلیل احساسات، حذف نویز و غیره پوشش می دهد. این پروژه ها از شبکه‌هایی با حافظه کوتاه‌مدت و شبکه‌های عصبی سیامی استفاده می کنند.

 اگر به دنبال ایجاد یک نمونه کار قدرتمند یادگیری ماشینی با پروژه های یادگیری عمیق هستید، این کتاب را بخوانید. این مقاله یک شبکه عصبی را از ابتدا بدون هیچ کتابخانه یادگیری عمیق مانند TensorFlow می سازد. من باورمندم که درک عملکرد درونی یک شبکه عصبی برای هر کسی که مشتاق به یادگیری علم داده است، مهم است. امیدوارم این مقاله برای شما مفید باشد.

شبکه عصبی چیست؟

بیشتر متون یادگیری مقدماتی شبکه های عصبی، همانندی های مغز انسان و شبکه های عصبی را در ابتدا آموزش می دهند. در این جا بدون پرداختن به این همانندی ها، اگر بخواهیم یک تعریف ساده داشته باشیم می توان گفت که شبکه های عصبی به عنوان یک تابع ریاضی که یک ورودی داده شده را به یک خروجی دلخواه نگاشت می کند، هستند. شبکه های عصبی از اجزای زیر تشکیل شده اند:

• یک لایه ورودی، x
• مقدار دلخواه برای لایه های پنهان
• یک لایه خروجی، ŷ
• مجموعه ای از وزن ها و بایاس ها برای هر لایه که با نام های W و b نشان داده می شوند
• انتخاب یک تابع فعال سازی برای هر لایه پنهان به نام σ. در این آموزش، از یک تابع فعال سازی Sigmoid استفاده می کنیم.

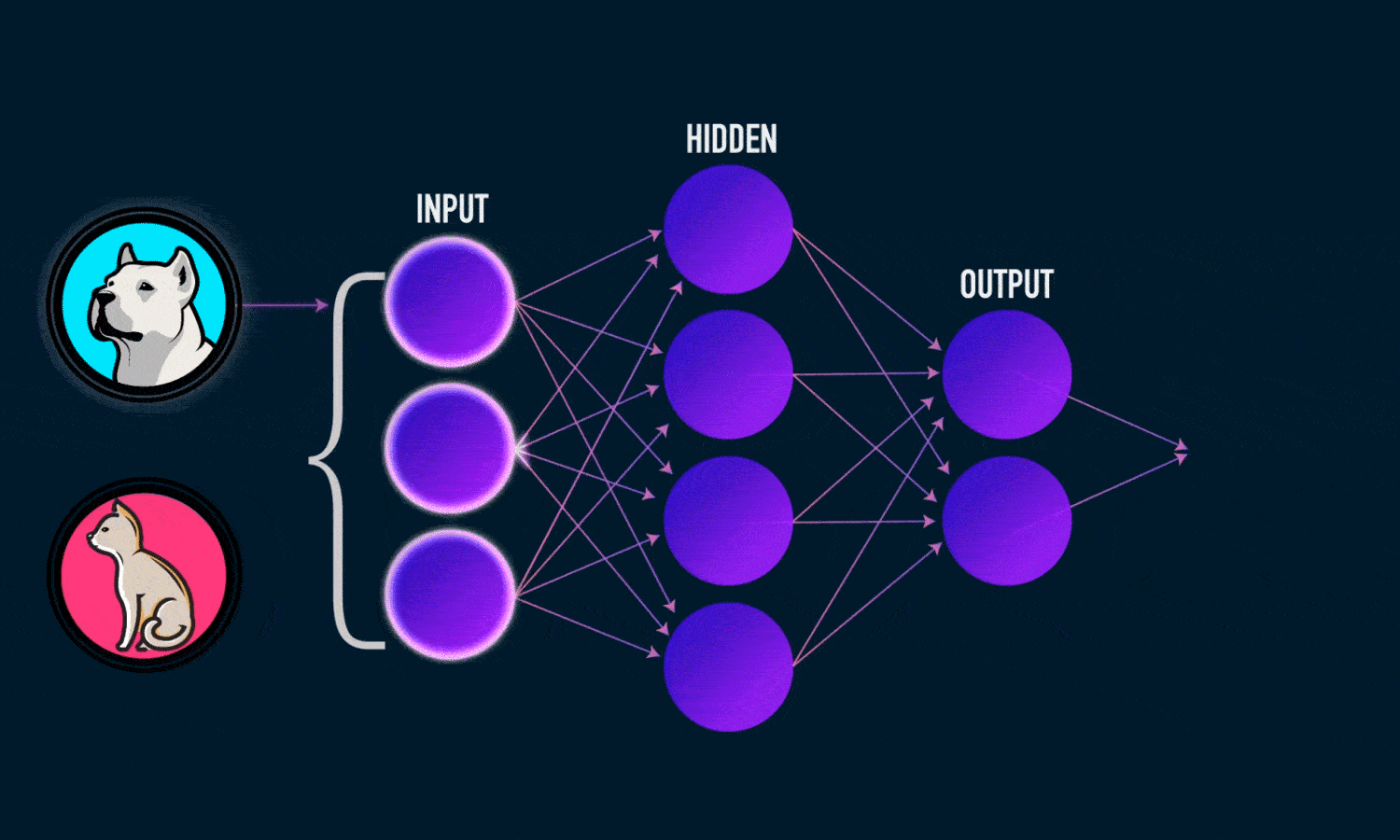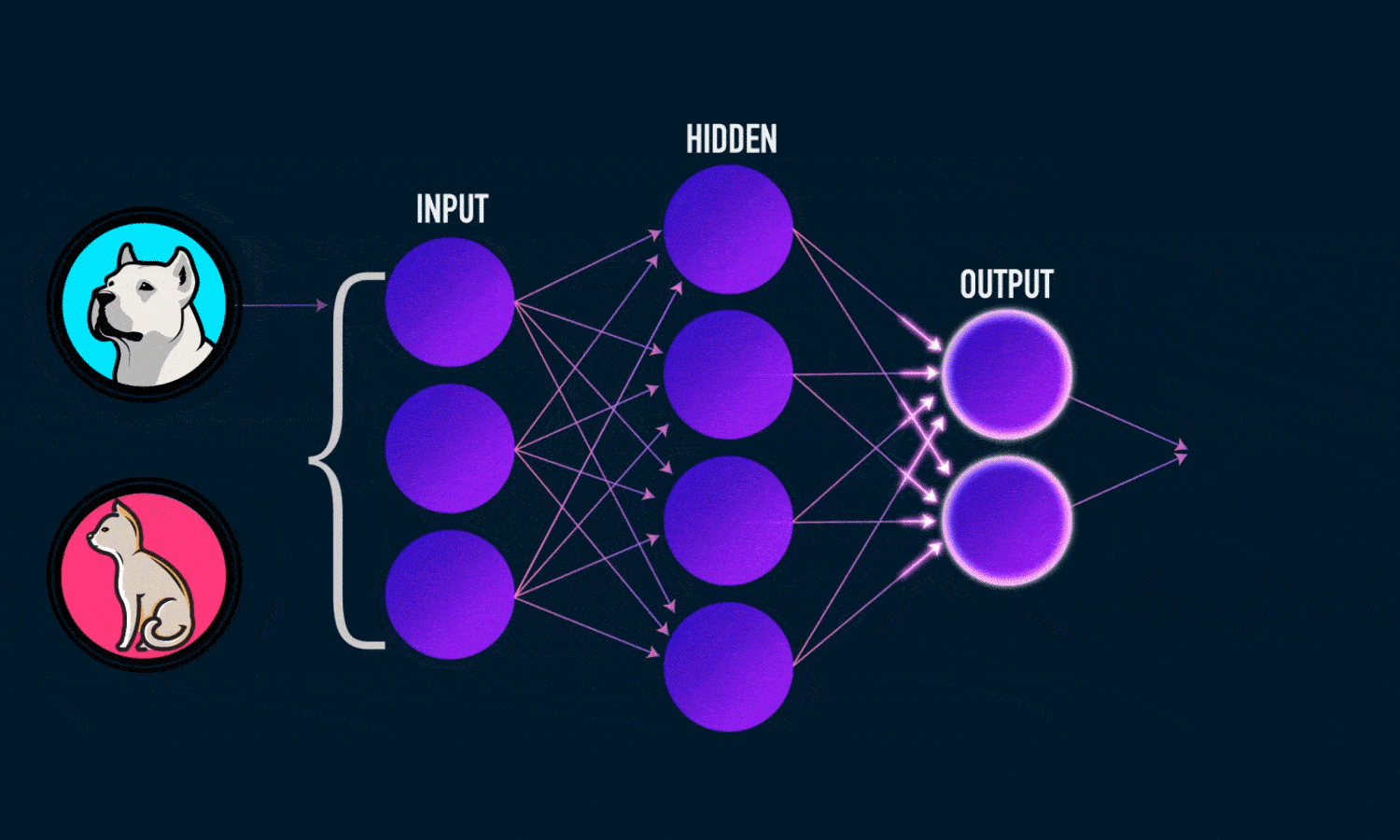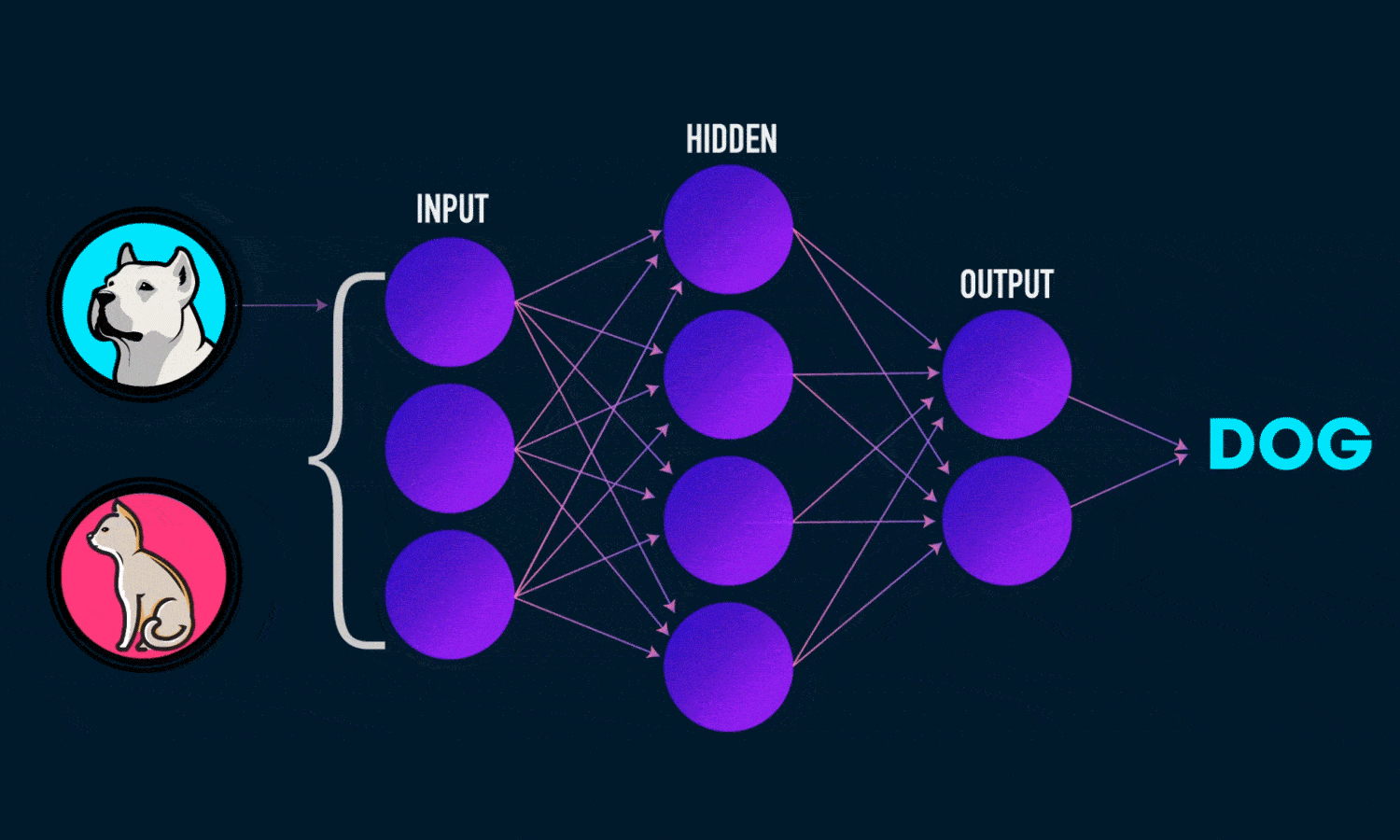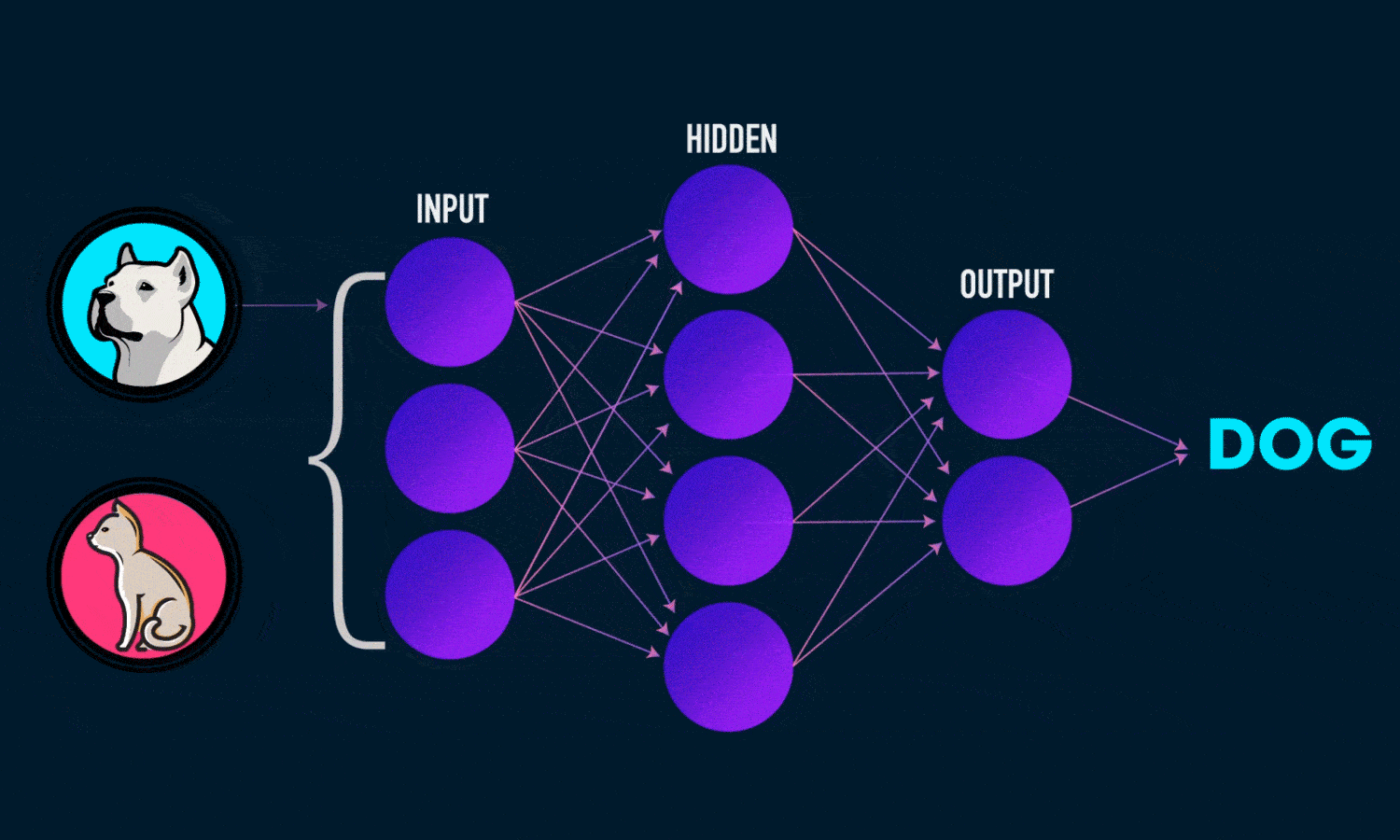
نمودار زیر معماری یک شبکه عصبی دو لایه را نشان می دهد (توجه داشته باشید که لایه ورودی معمولا هنگام شمارش تعداد لایه ها در یک شبکه عصبی حذف می شود)

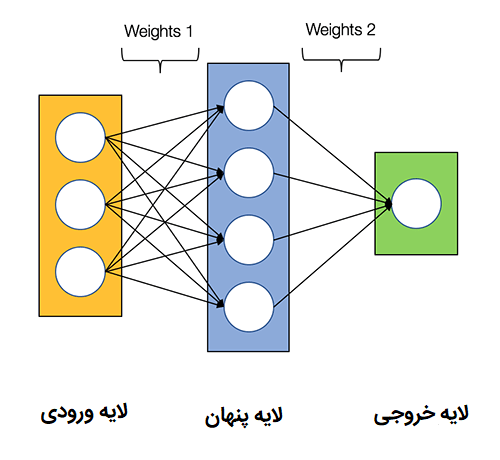
ایجاد کلاس شبکه عصبی در پایتون آسان است:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(y.shape)

آموزش دادن شبکه عصبی

خروجی ŷ یک شبکه عصبی دو لایه ساده به صورت زیر است:

ممکن است متوجه شوید که در معادله بالا، وزن‌های W و بایاس‌های b تنها متغیرهایی هستند که بر خروجی ŷ تاثیر می‌گذارند. به طور طبیعی، مقادیر مناسب برای وزن ها و بایاس ها، قدرت پیش بینی ها را تعیین می کند. فرآیند تنظیم دقیق وزن ها و بایاس ها از داده های ورودی به عنوان آموزش شبکه عصبی شناخته می شود.

هر تکرار فرآیند آموزشی شامل مراحل زیر است:

• محاسبه خروجی پیش بینی شده ŷ که به عنوان پیش خور(feedforward) شناخته می شود
• به روز رسانی وزن ها و بایاس ها که با نام پس انتشار (backpropagation) شناخته می شود.

نمودار زیر روند کار را نشان می دهد.

پیشخور (feedforward)

همان طور که در نمودار متوالی بالا مشاهده کردیم، پیشخور فقط یک حساب ساده است و برای یک شبکه عصبی دو لایه اصلی، خروجی شبکه عصبی به صورت زیر است:

بیایید یک تابع پیشخور در کد پایتون خود اضافه کنیم تا این کار را انجام دهیم. توجه داشته باشید که برای سادگی، بایاس ها را 0 فرض کرده ایم:

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

با این حال، هنوز به راهی برای ارزیابی «درستی» پیش‌بینی‌هایمان نیاز داریم (یعنی پیش‌بینی‌های ما چقدر دور از واقعیت هستند)؟ تابع Loss به ما این امکان را می دهد که این کار را انجام دهیم.

تابع Loss

توابع زیان یا Loss زیادی وجود دارد، و ماهیت مشکل ما باید انتخاب تابع ضرر را تعیین کند. در این آموزش، از یک خطای مجموع مربعات ساده به عنوان تابع ضرر استفاده خواهیم کرد.

یعنی خطای مجموع مربعات به سادگی مجموع تفاوت بین هر مقدار پیش بینی شده و مقدار واقعی است. این اختلاف مجذور می شود تا قدر مطلق تفاوت را اندازه گیری کنیم. هدف ما در آموزش شبکه عصبی یافتن بهترین مجموعه وزنه ها و بایاس هایی است که تابع Loss را به حداقل می رساند.

پس‌انتشار

اکنون که خطای پیش‌بینی (loss) خود را اندازه‌گیری کرده‌ایم، باید راهی برای انتشار مجدد خطا و به‌روزرسانی وزن‌ها و بایاس‌های خود پیدا کنیم.

برای دانستن مقدار مناسب برای تنظیم وزن ها و بایاس ها، باید مشتق تابع ضرر را نسبت به وزن ها و بایاس ها بدانیم. از حساب دیفرانسیل و انتگرال به یاد بیاورید که مشتق یک تابع در واقع همان شیب خط مماس بر منحنی تابع است.

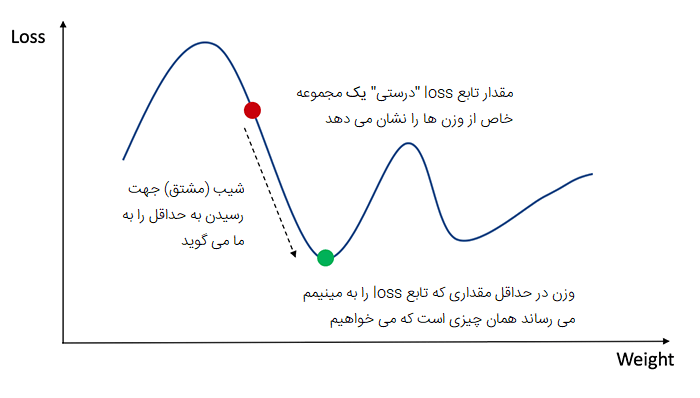
اگر مشتق را داشته باشیم، می‌توانیم به سادگی وزن‌ها و بایاس‌ها را با افزایش/کاهش از آن به‌روزرسانی کنیم (به نمودار بالا نگاه کنید). به این کار نزول گرادیان می گویند.

با این حال، نمی‌توانیم مستقیما مشتق تابع loss نسبت به وزن‌ها و بایاس‌ها را محاسبه کنیم، زیرا معادله تابع loss حاوی وزن‌ها و بایاس‌ها نیست. بنابراین، ما به قانون زنجیره ای نیاز داریم تا به ما در محاسبه آن کمک کند.

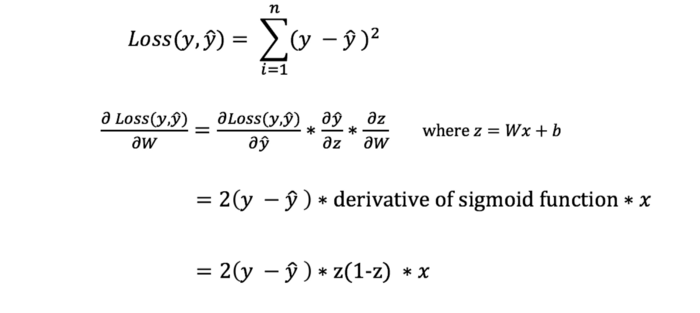
قانون زنجیره ای برای محاسبه مشتق تابع loss نسبت به وزن ها. توجه داشته باشید که برای سادگی، مشتق جزئی را با فرض یک شبکه عصبی 1-لایه نمایش داده ایم.

مشتق (شیب) تابع loss نسبت به وزن‌ها، تا بتوانیم وزن‌ها را مطابق با آن تنظیم کنیم. اکنون که آن را داریم، اجازه دهید تابع پس انتشار را به کد پایتون خود اضافه کنیم.

class NeuralNetwork:
    def __init__(self, x, y):
        self.input      = x
        self.weights1   = np.random.rand(self.input.shape[1],4) 
        self.weights2   = np.random.rand(4,1)                 
        self.y          = y
        self.output     = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T,  (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))

        # update the weights with the derivative (slope) of the loss function
        self.weights1 += d_weights1
        self.weights2 += d_weights2

برای درک ژرف تر از کاربرد حساب دیفرانسیل و انتگرال و قانون زنجیره ای در پس انتشار، به شدت این آموزش توسط که 3Blue1Brown ارائه شده است را توصیه می کنم. می توانید این آموزش را در نشانی ببینید.

چیدمان همگی در کنارهم

اکنون که کد پایتون کامل خود را برای انجام پیشخور و پس انتشار داریم، بیایید شبکه عصبی خود را با یک مثال به کار بگیریم و ببینیم که کارکرد آن چگونه است.

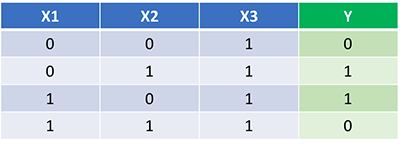
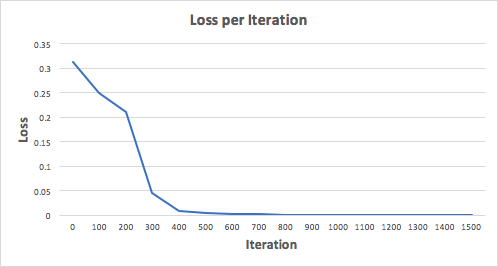
شبکه عصبی ما باید مجموعه ایده آل وزن ها را برای نشان دادن این تابع یاد بگیرد. بیایید شبکه عصبی را برای 1500 تکرار آموزش دهیم و ببینیم چه اتفاقی می‌افتد. با نگاهی به نمودار loss یا زیان در هر تکرار زیر، به وضوح می‌توانیم کاهش یکنواختی ضرر را به سمت حداقل مشاهده کنیم. این با الگوریتم نزول گرادیان که قبلا بحث کردیم، سازگار است.

بیایید به پیش بینی نهایی (خروجی) شبکه عصبی پس از 1500 تکرار نگاه کنیم.

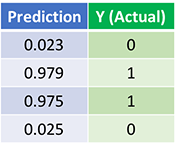
کار تمام شد. الگوریتم پیشخور و پس انتشار ما شبکه عصبی را با موفقیت آموزش داد و پیش‌بینی‌ها بر روی مقادیر واقعی همگرا شدند.

توجه داشته باشید که تفاوت جزئی بین پیش بینی ها و مقادیر واقعی وجود دارد. این مطلوب است، زیرا از برازش بیش از حد جلوگیری می کند و به شبکه عصبی اجازه می دهد تا داده های دیده نشده را بهتر تعمیم دهد.

گام های بعدی در خصوص ساخت شبکه عصبی در پایتون

خوشبختانه برای ما، سفر ما تمام نشده است. هنوز چیزهای زیادی برای یادگیری در مورد شبکه های عصبی و یادگیری عمیق وجود دارد. مثلا:

• به جز تابع Sigmoid از چه تابع فعال سازی دیگری می توانیم استفاده کنیم؟
• استفاده از نرخ یادگیری هنگام آموزش شبکه عصبی
• استفاده از کانولوشن برای کارهای طبقه بندی تصویر

منبع: وب سایت towardsdatascience